Floor Function Excel
Floor Function Excel - When i write \\lfloor\\dfrac{1}{2}\\rfloor the floors come out too short to cover the fraction. The number of samples is the number of lines plus one for an additional end point: Is there a convenient way to typeset the floor or ceiling of a number, without needing to separately code the left and right parts? How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. How can i lengthen the floor symbols? If you need even more general input involving infix operations, there is the floor function. 4 i suspect that this question can be better articulated as: \end{axis} \end{tikzpicture} \end{document} the sample points are marked. The correct answer is it depends how you define floor and ceil. I understand what a floor function does, and got a few explanations here, but none of them had a explanation, which is what i'm after. For example, is there some way to do $\\ceil{x}$ instead of $\\lce. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. Is there a macro in latex to write ceil(x) and floor(x) in short form? You could define as shown here the more common way with always. When i write \\lfloor\\dfrac{1}{2}\\rfloor the floors come out too short to cover the fraction. The number of samples is the number of lines plus one for an additional end point: What are some real life application of ceiling and floor functions? I understand what a floor function does, and got a few explanations here, but none of them had a. What are some real life application of ceiling and floor functions? The most natural way to specify the usual principal branch of the arctangent function basically uses the idea of the floor function anyway, so your formula for the floor. 4 i suspect that this question can be better articulated as: It natively accepts fractions such as 1000/333 as input,. Googling this shows some trivial applications. \end{axis} \end{tikzpicture} \end{document} the sample points are marked. You could define as shown here the more common way with always rounding downward or upward on the number line. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. For example, is there. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. 4 i suspect that this question can be better articulated as: It natively accepts fractions such as 1000/333 as input, and scientific notation such as 1.234e2; Can someone explain to me what is going. The correct answer is. Googling this shows some trivial applications. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. The correct answer is it depends how you define floor and ceil. The number of samples is the number of lines plus one for an additional end point: When i write \\lfloor\\dfrac{1}{2}\\rfloor. It natively accepts fractions such as 1000/333 as input, and scientific notation such as 1.234e2; Can someone explain to me what is going. I understand what a floor function does, and got a few explanations here, but none of them had a explanation, which is what i'm after. Is there a macro in latex to write ceil(x) and floor(x) in. How can i lengthen the floor symbols? The long form \\left \\lceil{x}\\right \\rceil is a bit lengthy to type every time it is used. How can we compute the floor of a given number using real number field operations, rather than by exploiting the printed notation,. Is there a macro in latex to write ceil(x) and floor(x) in short form?. I understand what a floor function does, and got a few explanations here, but none of them had a explanation, which is what i'm after. The number of samples is the number of lines plus one for an additional end point: If you need even more general input involving infix operations, there is the floor function. The correct answer is. What are some real life application of ceiling and floor functions? Googling this shows some trivial applications. The number of samples is the number of lines plus one for an additional end point: I understand what a floor function does, and got a few explanations here, but none of them had a explanation, which is what i'm after. If you.Excel FLOOR.PRECISE function Exceljet
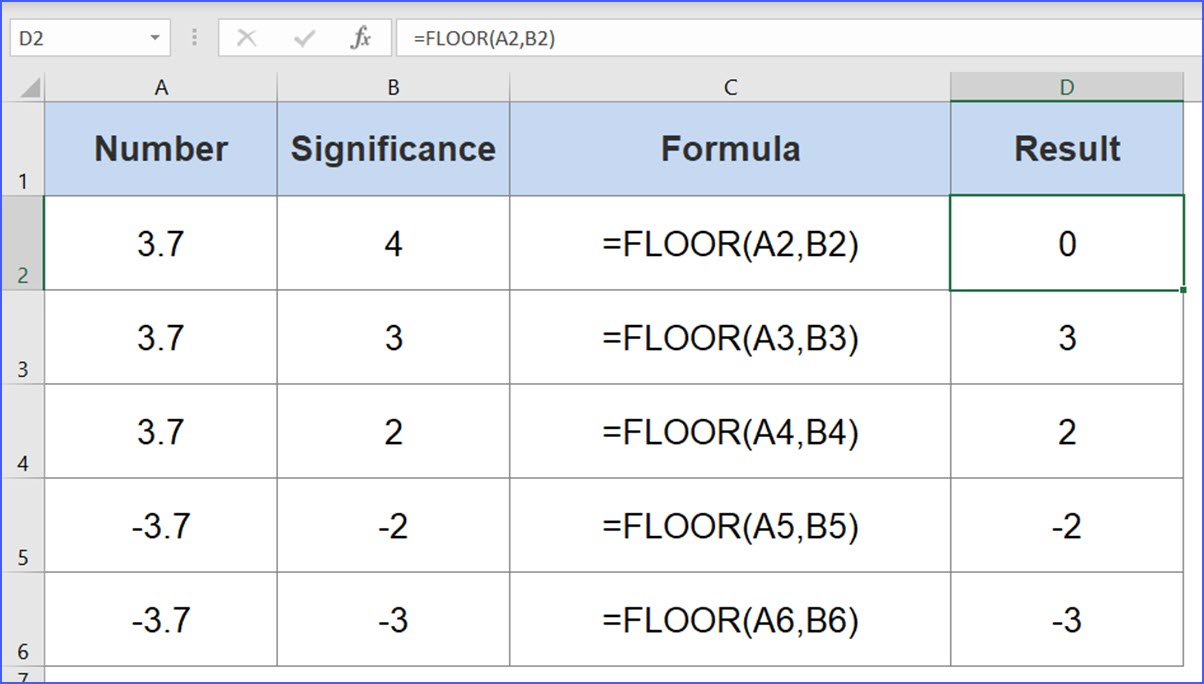
Excel FLOOR Function
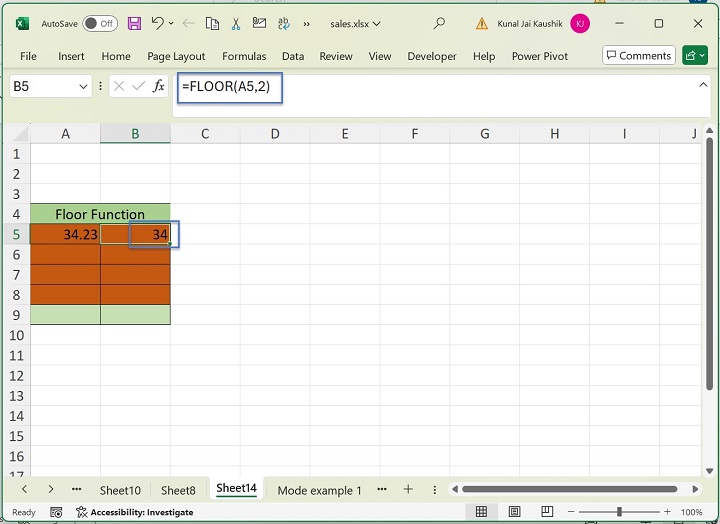
How to Use FLOOR Function ExcelNotes
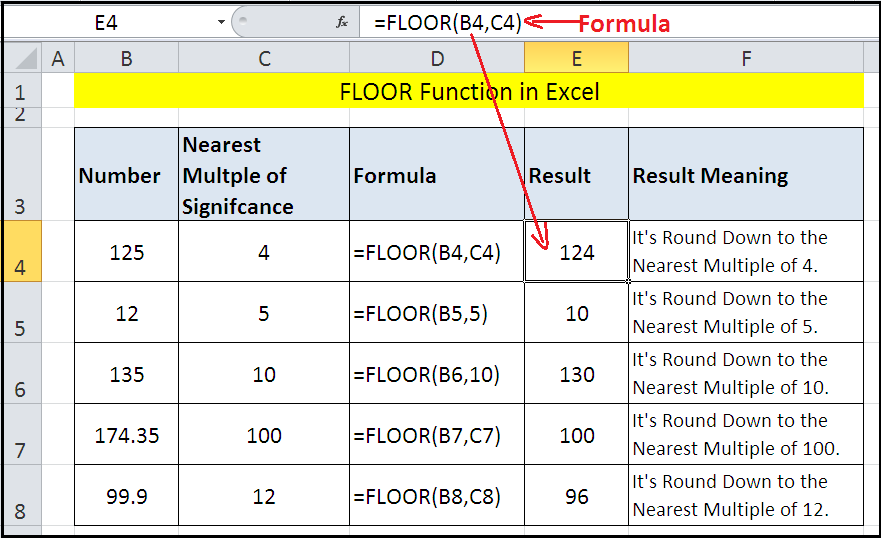
How To Use FLOOR Function ExcelDataPro
Excel FLOOR Function
How To Use The Floor Function In Excel Design Talk
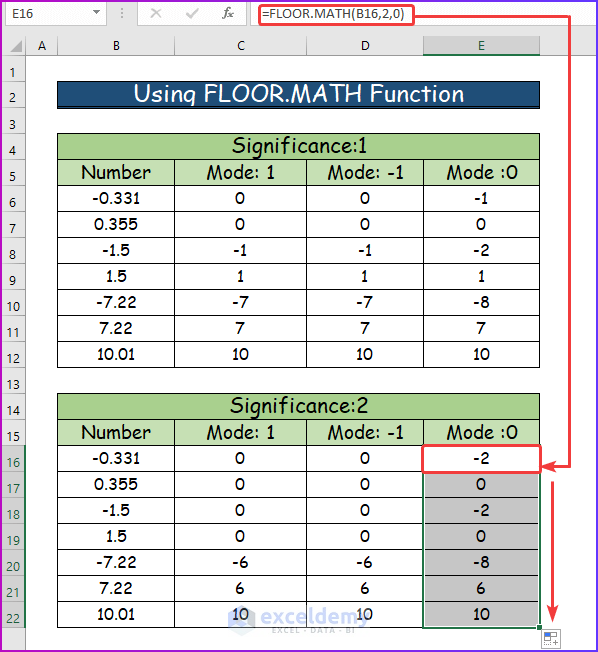
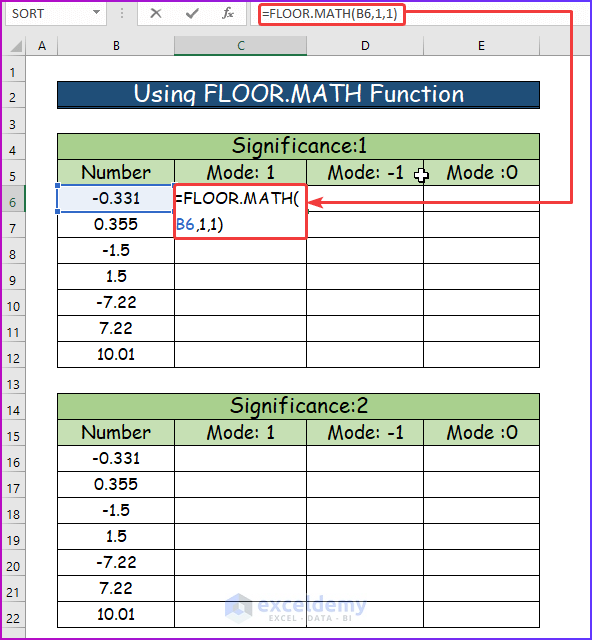
How to Use CEILING.MATH and FLOOR.MATH Functions in Excel
Excel FLOOR Function
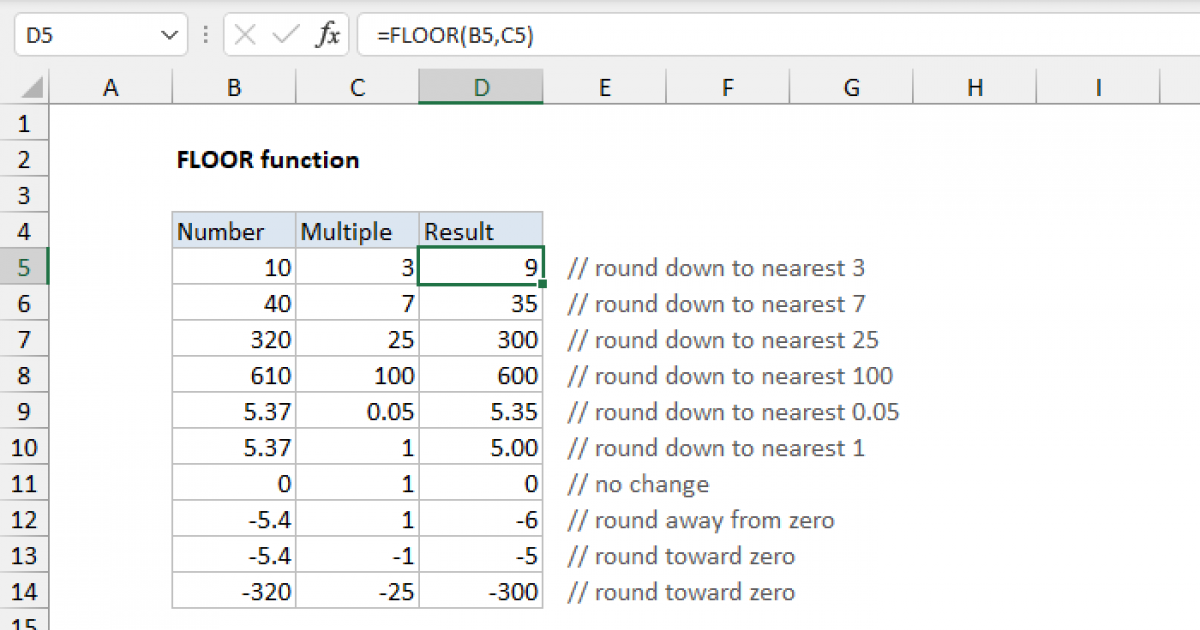
Excel FLOOR function Exceljet
How to Use CEILING.MATH and FLOOR.MATH Functions in Excel
Related Post: