Binom Dist Excel
Binom Dist Excel - Visual interpretation i think this proof is easiest to visualize on pascal's triangle. I gave this as a homework exercise once (after having given the theory for computing a binomial coefficient modulo two in terms of the binary expansions),. Can anyone help provide the most elementary/elegant proofs for the following. Upvoting indicates when questions and answers are useful. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. What's reputation and how do i. $\binom {3} {2}$ is calculating the number of ways to choose two objects out of a. I'm studying probability and statistics and had a question regarding notation. To gain full voting privileges, I'm studying probability and statistics and had a question regarding notation. 1 $\binom {3} {1}$ is calculating the number of ways to choose one object out of a set of three. What's reputation and how do i. Can anyone help provide the most elementary/elegant proofs for the following. There are several ways to show this. To gain full voting privileges, $\binom {3} {2}$ is calculating the number of ways to choose two objects out of a. Upvoting indicates when questions and answers are useful. There are several ways to show this. What's reputation and how do i. Can anyone help provide the most elementary/elegant proofs for the following. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. I gave this as a homework exercise once (after having given the theory for computing a binomial coefficient modulo two in terms of the binary expansions),. Upvoting indicates when questions and answers. The largest root of $\sum_ {k=0}^n\cos\left (\frac {k\pi} {2}\right)\binom {n} {k}x^k$ is approximately $\frac {n} {\pi}$ or $\frac {2n} {\pi}$. Visual interpretation i think this proof is easiest to visualize on pascal's triangle. Can anyone help provide the most elementary/elegant proofs for the following. I'm studying probability and statistics and had a question regarding notation. You'll need to complete a. Let's look at these identities graphically on pascal's triangle: $\binom {3} {2}$ is calculating the number of ways to choose two objects out of a. I gave this as a homework exercise once (after having given the theory for computing a binomial coefficient modulo two in terms of the binary expansions),. Can anyone help provide the most elementary/elegant proofs for. I'm studying probability and statistics and had a question regarding notation. Upvoting indicates when questions and answers are useful. Visual interpretation i think this proof is easiest to visualize on pascal's triangle. Let's look at these identities graphically on pascal's triangle: You'll need to complete a few actions and gain 15 reputation points before being able to upvote. Upvoting indicates when questions and answers are useful. Let's look at these identities graphically on pascal's triangle: $\binom {3} {2}$ is calculating the number of ways to choose two objects out of a. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. I found some combinatorial identities in my old notebooks, but. You'll need to complete a few actions and gain 15 reputation points before being able to upvote. Let's look at these identities graphically on pascal's triangle: I found some combinatorial identities in my old notebooks, but i cannot recall how i derived them. Upvoting indicates when questions and answers are useful. I noticed that combinations and the binomial coefficient are. The largest root of $\sum_ {k=0}^n\cos\left (\frac {k\pi} {2}\right)\binom {n} {k}x^k$ is approximately $\frac {n} {\pi}$ or $\frac {2n} {\pi}$. What's reputation and how do i. I found some combinatorial identities in my old notebooks, but i cannot recall how i derived them. You'll need to complete a few actions and gain 15 reputation points before being able to upvote.. Visual interpretation i think this proof is easiest to visualize on pascal's triangle. The largest root of $\sum_ {k=0}^n\cos\left (\frac {k\pi} {2}\right)\binom {n} {k}x^k$ is approximately $\frac {n} {\pi}$ or $\frac {2n} {\pi}$. I'm studying probability and statistics and had a question regarding notation. What's reputation and how do i. I noticed that combinations and the binomial coefficient are essentially.How to use the BINOM.DIST function
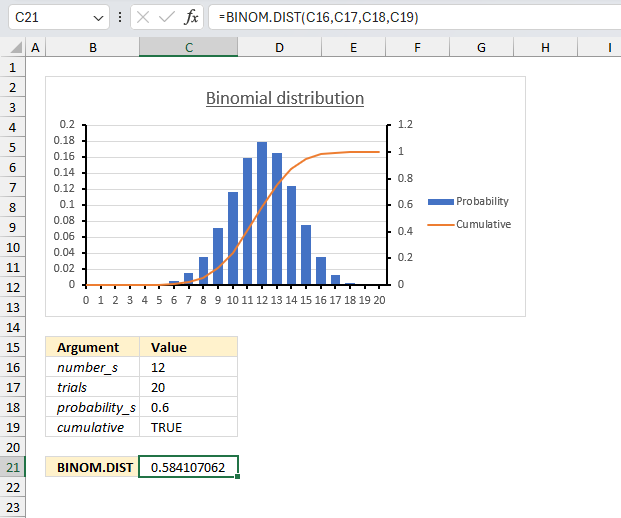
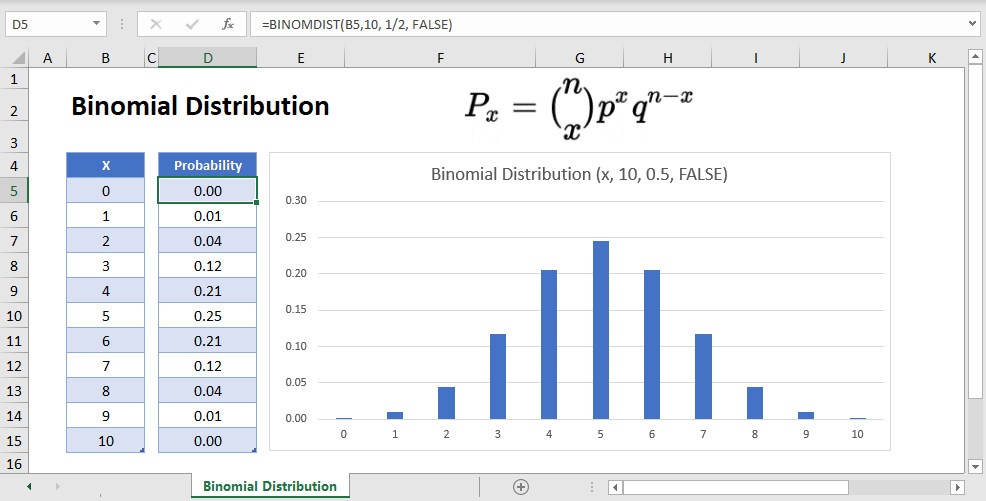
How To Create A Binomial Distribution Graph In Excel?
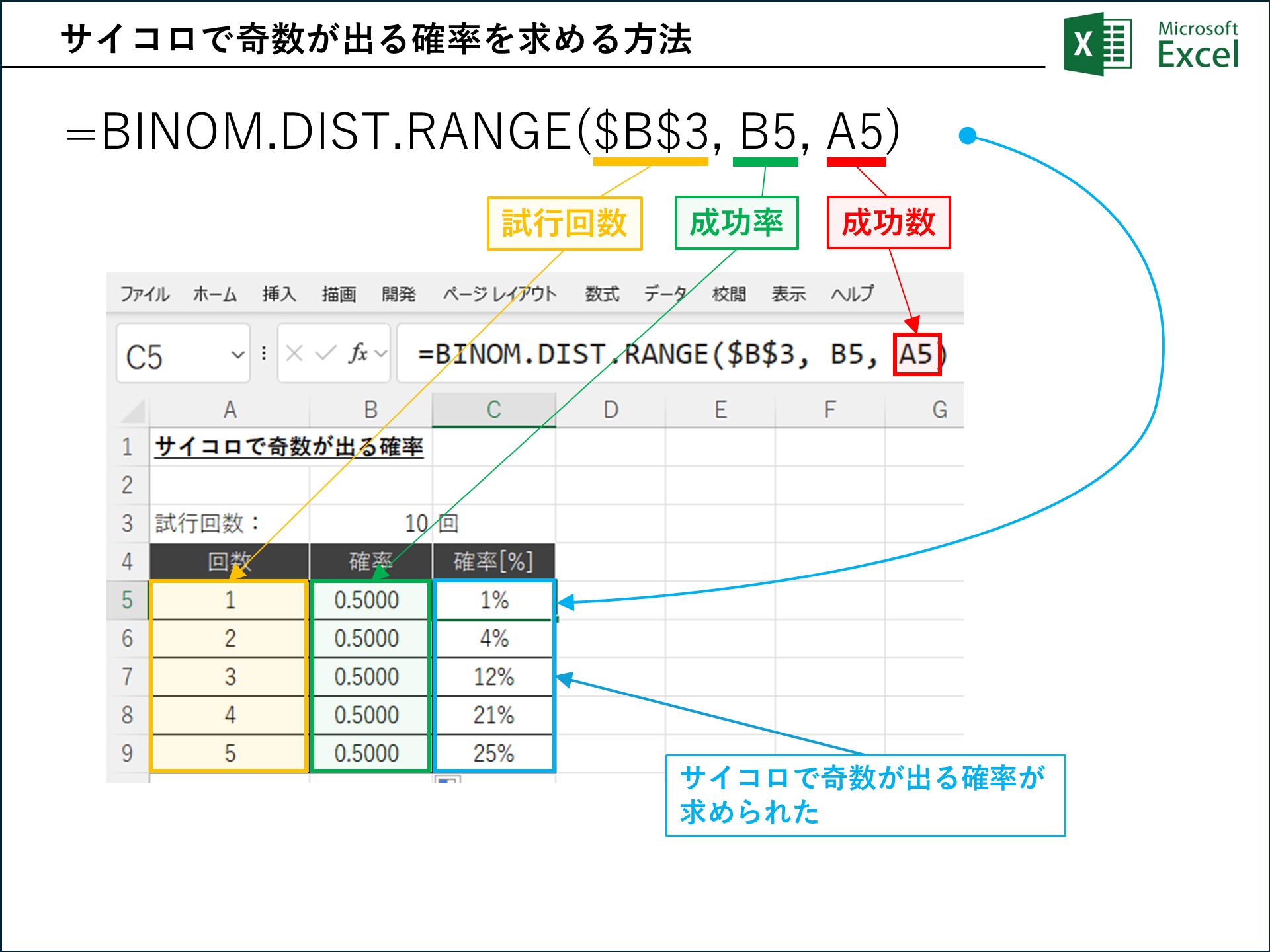
BINOM.DIST.RANGE Function in Excel Excel Unlocked
464|Excel BINOM.DIST.RANGE関数徹底解説:指定範囲の確率をまとめて計算! 関連関数もご紹介
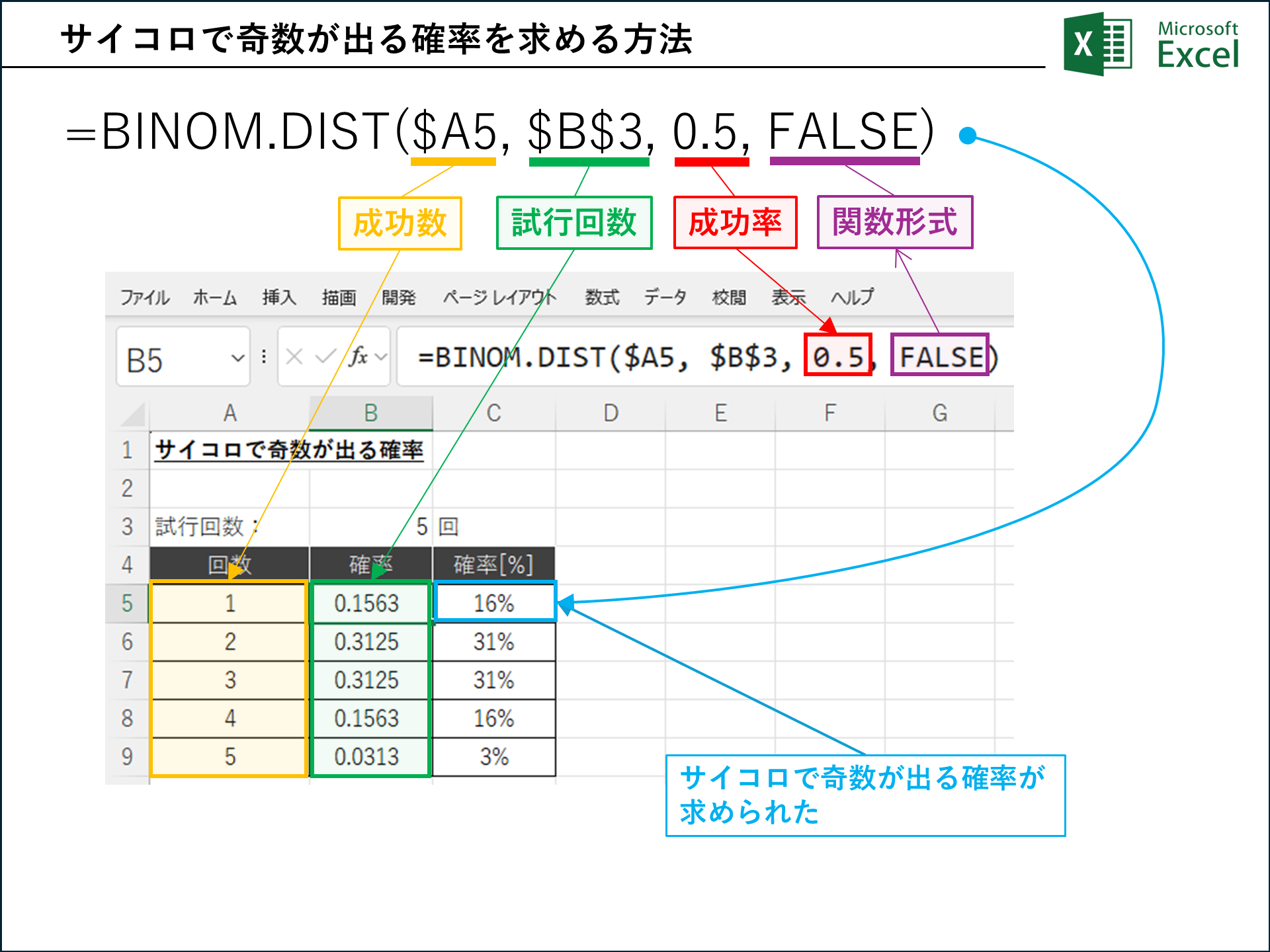
463|Excel BINOM.DIST/BINOMDIST関数徹底解説:サイコロの確率計算もラクラク!
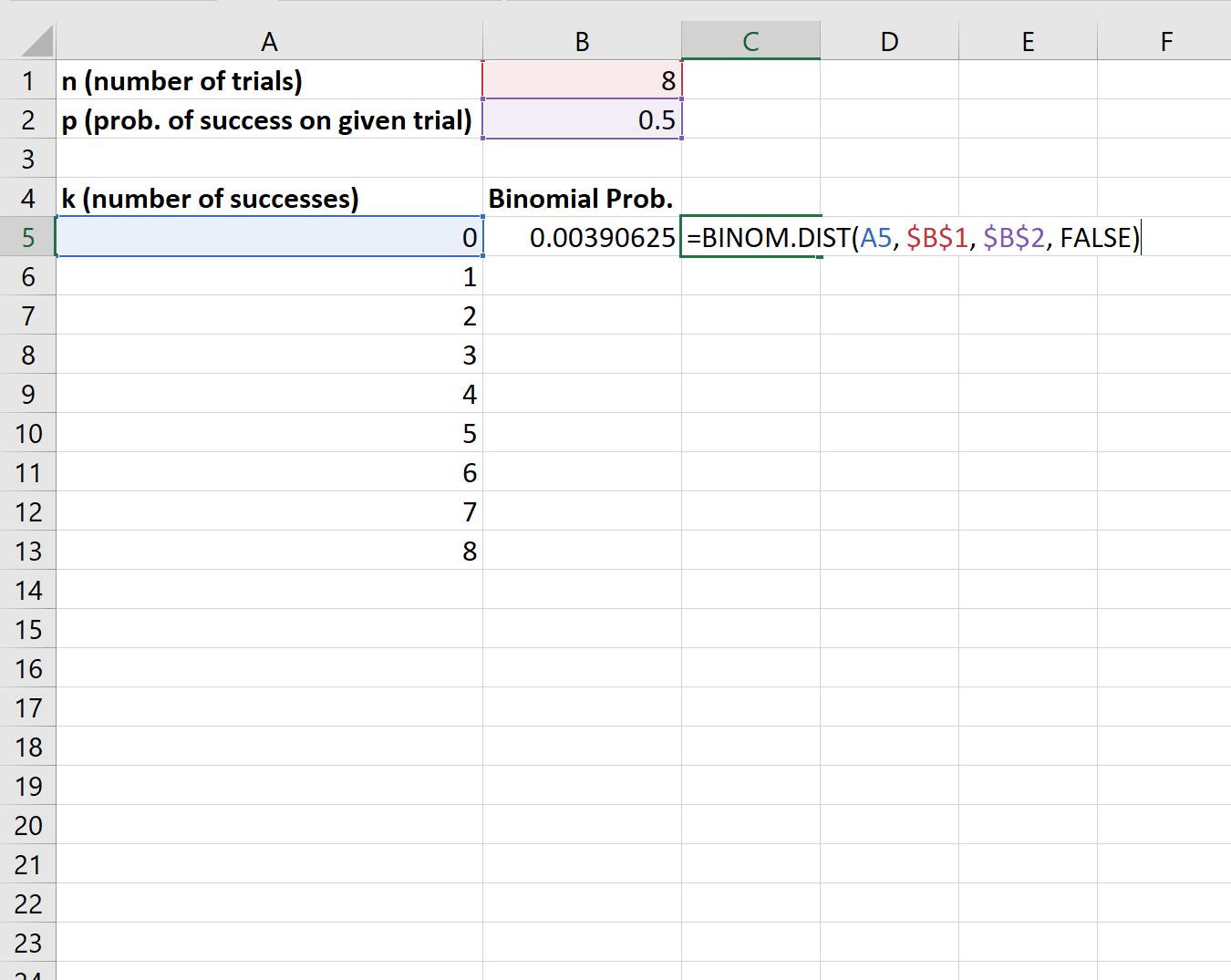
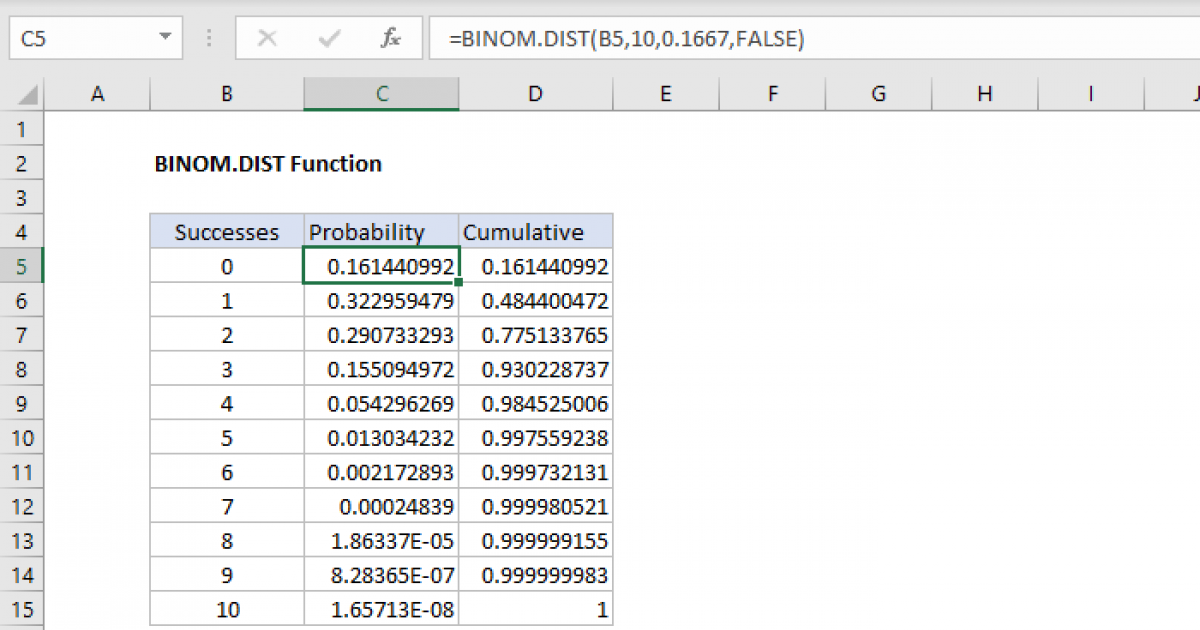
Excel BINOM.DIST function Exceljet
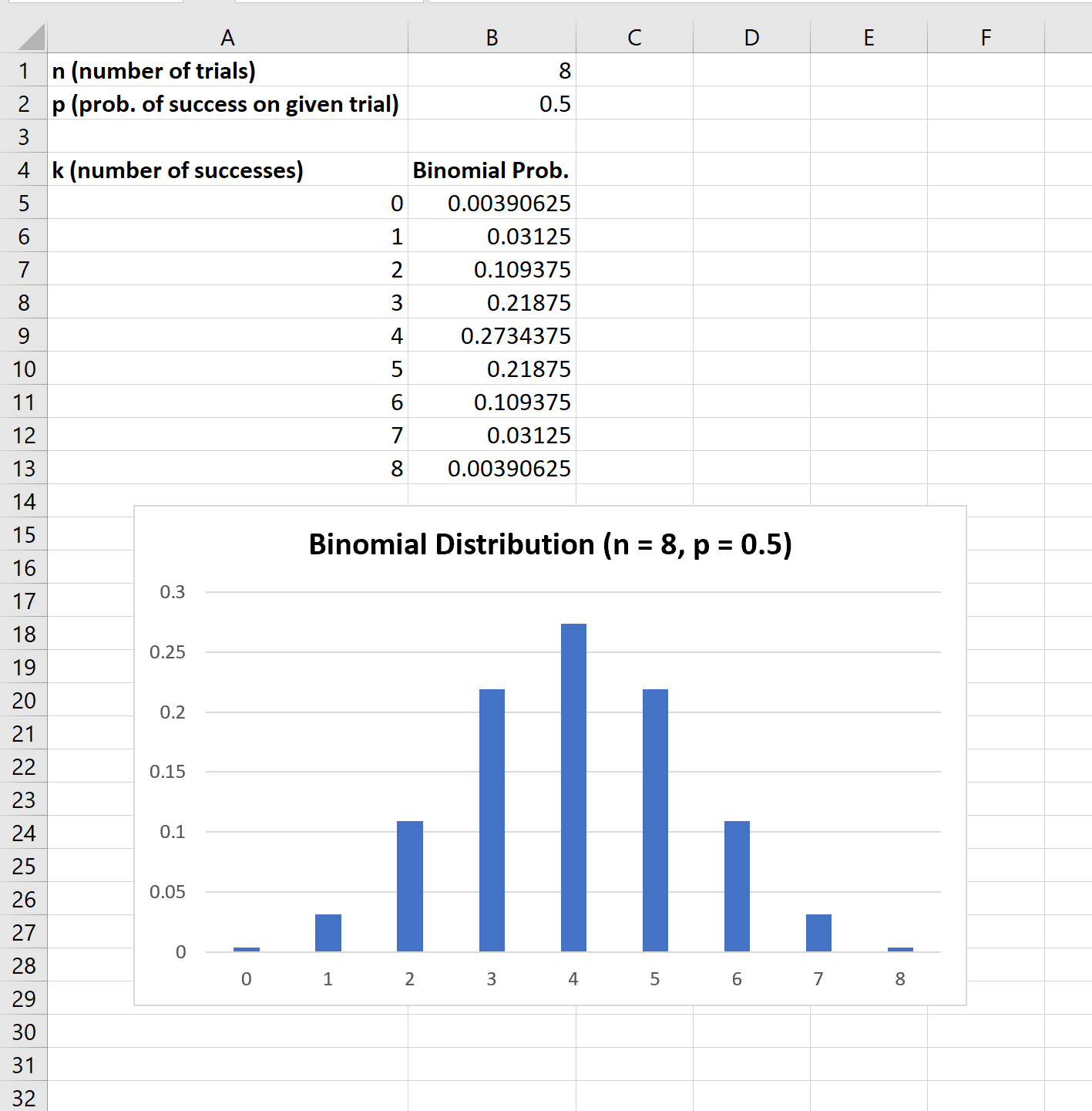
Binomial Distribution in Excel & Google Sheets Automate Excel
How to Use Excel's Binomial Distribution Function =BINOM.DIST YouTube
How To Create A Binomial Distribution Graph In Excel?
Excel Magic Trick 1209 BINOM.DIST.RANGE Function for Calculating
Related Post: